특정 리스트를 정렬하는 방법에는 여러 가지가 있다.
그중에서도 대표적으로 분할 정복을 활용하여 리스트를 정렬하는 것이 합병 정렬, 퀵 정렬이다.
그 중 합병 정렬에 대해 알아보자. 합병 정렬은 병합 정렬이라고도 불린다.
정렬된 두 리스트의 합 정렬
먼저 알아야 할 것이 있다. 합병 정렬은 정렬된 임의의 두 리스트가 있을 때, 두 리스트를 합치면서 정렬하기 위해서는 두 리스트의 성분을 처음부터 하나씩 비교해면서 새로운 리스트에 넣어주다가 둘 중 어느 한 리스트의 성분 모두 없어지면, 나머지는 그냥 새로운 리스트의 뒤에 들어가면 된다.
ex. [1,2,3,5] [4,6,7,8]이 있을 때 이를 합치면서 정렬하려 한다. 처음부터 성분을 비교하면서 넣다 보면 어느 순간 새로운 리스트에 [1,2,3,4,5]까지 들어가고 두 리스트가 [] [6,7,8] 상태가 될 것이다. 이때 남은 리스트에 있는 6,7,8 성분은 그냥 새로운 리스트 [1,2,3,4,5] 뒤에 붙여 [1,2,3,4,5,6,7,8]를 만들어주면 된다.
이러한 정렬된 임의의 두 리스트를 합칠 때의 과정에서 분할 정복의 개념을 더해 착안해 낸 것이 합병 정렬이다.
합병 정렬의 과정
리스트를 먼저 나눈다.(divide) 그리고 각각의 문제를 해결해야 하는데 여기서는 분할 정복을 반복해서 활용해야 하므로 리스트의 길이가 1이 될 때까지 문제를 나눠준다.(conquer) 리스트의 길이가 1일 경우 각각의 나눈 리스트를 더한다.(combine) 리스트를 더할 때는 위에서 본 '정렬된 두 리스트의 합 정렬'과정으로 더한다. combine 되는 리스트는 그 길이가 1일지라도 최소한 정렬된 알고리즘이기 때문에 정상적으로 정렬될 수 있다.
cf. 분할 정복의 3단계는 divide, conquer, combine이라고 했다. 하지만 이 셋만큼이나 중요한 것이 또 하나 있는데, 바로 base-case의 설정이다. base-case를 제대로 설정해주지 않으면 재귀를 활용한 분할 정복이 제대로 이뤄지지 않을 것이다. 위에서는 리스트의 길이가 1이 되었을 때가 base-case이다.
합병 정렬 구현 (by. C++)
#include <stdio.h>
int number = 8;
int size;
int sorted[8]; // 정렬할 때 사용할 배열, 해당 배열은 반드시 전역 변수로 선언
int count = 0;
void merge(int a[], int m, int middle, int n) {
int i = m;
int j = middle + 1;
int k = m;
// 작은 순서대로 배열에 삽입
while(i <= middle && j <= n) {
if(a[i] <= a[j]) {
sorted[k] = a[i];
i++;
} else {
sorted[k] = a[j];
j++;
}
k++;
}
// 남은 데이터 삽입
if(i > middle) {
for(int t = j; t <= n; t++) {
sorted[k] = a[t];
k++;
}
} else {
for(int t = i; t <= middle; t++) {
sorted[k] = a[t];
k++;
}
}
// 정렬된 배열을 원래의 배열에 삽입
for(int t = m; t <= n; t++) {
a[t] = sorted[t];
}
}
void mergeSort(int a[], int m, int n) {
// 이외의 경우는 크기가 1개인 경우
if(m < n) {
int middle = (m + n) / 2;
mergeSort(a, m, middle);
mergeSort(a, middle + 1, n);
merge(a, m, middle, n);
}
}
int main(void) {
int array[number] = {7, 6, 5, 8, 3, 5, 9, 1};
mergeSort(array, 0, number - 1);
for(int i = 0; i < number; i++) {
printf("%d ", array[i]);
}
} 합병 정렬 구현 (by. python)
def combine(num_list, start_idx, mid_idx, end_idx):
l_idx = start_idx # start_idx ~ mid_idx
r_idx = mid_idx+1 # mid_idx+1 ~ end_idx
sorted_list = []
while l_idx <= mid_idx and r_idx <= end_idx:
# if l_idx > mid_idx:
# # sorted_list.append(num_list[r_idx])
# # r_idx += 1
# sorted_list += num_list[r_idx:end_idx+1]
# r_idx = end_idx + 1
# elif r_idx > end_idx:
# # sorted_list.append(num_list[l_idx])
# # l_idx += 1
# sorted_list += num_list[l_idx:mid_idx+1]
# l_idx = mid_idx + 1
if num_list[l_idx] < num_list[r_idx]:
sorted_list.append(num_list[l_idx])
l_idx += 1
else:
sorted_list.append(num_list[r_idx])
r_idx += 1
sorted_list += num_list[r_idx:end_idx+1]
sorted_list += num_list[l_idx:mid_idx+1]
num_list[start_idx:end_idx+1] = sorted_list
def bottom_up_merge_sort(num_list):
size = 1
while size < len(num_list):
start_idx = 0
while start_idx < len(num_list):
end_idx = min(start_idx + size * 2 - 1, len(num_list)-1)
mid_idx = min(start_idx + size - 1, end_idx)
combine(num_list, start_idx, mid_idx, end_idx)
print(num_list)
start_idx = end_idx + 1
size *= 2
n = int(input())
num_list = []
for _ in range(n):
num_list.append(int(input()))
bottom_up_merge_sort(num_list)합병 정렬 과정 이미지
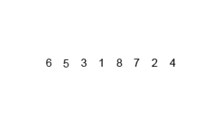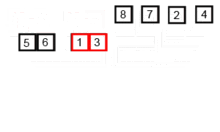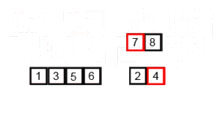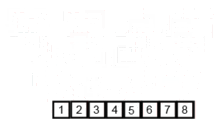
'💻 CS > 자료구조 & 알고리즘' 카테고리의 다른 글
| [자료구조] 선택정렬(Selection Sort)의 증명 (0) | 2020.04.02 |
|---|---|
| [자료구조] 자료구조개론 (0) | 2020.03.26 |
| [알고리즘] 비트연산자를 활용하여 부분집합 만들기 (1) | 2020.02.01 |
| [알고리즘] 완전검색 (Brute force) (0) | 2020.01.28 |
| [알고리즘] Greedy Algorithm (0) | 2020.01.22 |