최단 경로 알고리즘
- 가장 짧은 경로를 찾는 알고리즘
- 대표적으로 3가지 케이스가 존재한다.
- 한 지점에서 다른 한 지점까지 도달할 수 있는 최단경로 / 한 지점에서 다른 모든 지점까지 도달할 수 있는 최단경로 / 모든 지점에서 다른 모든 지점까지 도달할 수 있는 최단경로
- 그래프를 통해 지점과 연결거리를 표현한다는 특징이 있다.
다익스트라 최단거리 알고리즘
개념
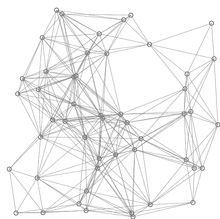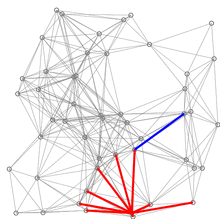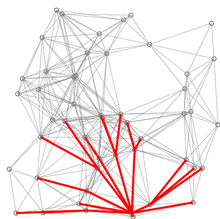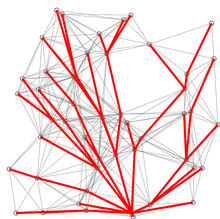
- 특정노드에서 다른 모든 노드로 가는 최단 경로를 계산한다.
- 음의 거리가 없어야한다는 조건이 존재한다
- 다익스트라 알고리즘은 그리디 알고리즘의 일종이라고 할 수도 있다. (매 상황에서 가장 비용이 적은 노드를 선택하는 과정을 반복하기 때문)
동작과정
- 출발노드 설정
- 최단 거리 테이블 초기화 (주어진 정보 외엔 모두 무한(최대값)으로, 자기자신은 0으로 임의설정)
- 방문하지 않은 노드 중 최단거리가 가장 짧은 노드 선택
- 해당 노드를 거쳐 다른 노드로 가는 비용을 계산해 최단거리 테이블 갱신
- 3과 4를 반복 수행
실질적 문제해결 과정
- 입력으로 각 지점끼리 연결된 거리에 대한 정보가 주어진다.
- 주어진 거리 정보를 hash(dictionary) 등의 방식을 이용해 저장해놓는다. (=
graph) - 방문정보 확인을 위한 리스트를 생성하고 모두 0으로 초기화한다. (=
visit) 이 때 출발지점은 방문한 것으로 1로 처리한다. - 각 지점끼리의 최단거리정보를 저장하는 리스트를 생성하고 그 곳을 모두 무한으로 초기화한다. (=
distance) 출발지점 자신과의 거리는 0으로 처리한다. - 출발지점과 직접 연결된 지점과의 거리를
graph에서 확인해distance에 저장한다. distance에서 현재 방문하지 않은 지점 중 출발지점으로부터 가장 가까운 지점(=A)를 찾고, 이와 직접 연결된 지점(=B)들을 살펴본다. 이 때,A의 방문여부를 체크하여visit에서의 값을 1로 처리한다.- [출발지점에서
A까지의 거리 +A와B의 거리]가distance에 표기된 출발지점으로부터B의 최단거리보다 짧다면 이를 갱신한다. - 모든 노드를 갱신할때까지 5번과 6번 과정을 반복한다.
성능
- 모든 지점(노드)의 개수를 N이라고 하면, 모든 노드의 각 노드에 대한 거리를 확인해야 하기 때문에 전체 시간복잡도는 O(N^2)이다.
- 일반적으로 지점(노드)의 개수가 5000개 이하라면 방문하지 않은 노드 중 가장 가까운 노드를 찾는 과정이 포함되어도 괜찮다.
- 하지만 노드가 10000개를 넘어갈 경우 우선순위 큐(힙)를 사용하여 방문하지 않는 노드 중 가장 가까운 노드를 찾는 과정을 효율화하는 것이 좋다. 이 경우 연결거리의 개수를 E라고 했을 때 시간복잡도는 O(ElogN)이 된다. (단 연결거리가 중복해서 존재하는 경우는 제외)
- 우선순위 큐를 사용하면 방문여부를 체크할 필요가 없다는 특징이 있다.
실질적 문제해결 과정 : 힙자료구조를 사용한 경우
- 입력으로 각 지점끼리 연결된 거리에 대한 정보가 주어진다.
- 주어진 거리 정보를 hash(dictionary) 등의 방식을 이용해 저장해놓는다. (=
graph) - 각 지점끼리의 최단거리정보를 저장하는 리스트를 생성하고 그 곳을 모두 무한으로 초기화한다. (=
distance) 출발지점 자신과의 거리는 0으로 처리한다. - 출발지점 자기 자신을 (거리, 지점)의 튜플형식으로 우선순위 큐에 넣는다. 물론 출발지점 자신과의 거리는 0이다.
- 우선순위 큐에서 가장 앞에 있는 지점(A)을 꺼내
graph에서 그와 직접 연결된 지점들(B)들을 살펴본다. - [출발지점으로부터
A까지의 거리 +A에서B까지의 거리]가distance에 표기된 출발지점으로부터B의 최단거리보다 짧다면 이를 갱신하고 우선순위 큐에 이를 삽입한다. - 우선순위 큐에 아무런 값이 존재하지 않을 때까지 4번과 5번 과정을 반복한다.
플로이드 워셜 알고리즘
개념
- 모든 노드의 모든 노드에 대한 최단거리를 구할 수 있다.
- 방문하지 않은 노드 중 최단 거리를 갖는 노드를 찾는 과정이 필요 없다.
- 플로이드 워셜은 2차원 테이블에 최단거리 정보를 저장한다.
- 플로이드 워셜은 다이나믹 프로그래밍 유형에 속한다.
동작과정
- 각 단계마다 특정 노드(K)를 거쳐가는 경우를 확인하여 A에서 B로 직접가는 경우보다 A에서 K를 거쳐 B를 가는 경우가 더 빠른지 체크한다.
- 이를 모든 노드에 대해 수행한다.
실질적 문제해결 과정
- 입력으로 각 지점끼리 연결된 거리에 대한 정보가 주어진다.
- 모든 지점끼리의 거리를 표현한 2차원 리스트를 초기화한다. (=
graph) 이 때 자신과의 거리는 0이며 나머지는 모두 무한이다. - 주어진 연결된 거리에 대한 정보를 기반으로 2차원 리스트를 업데이트한다.
- 모든 지점에 대해 해당 지점(
K)를 거쳐가는 경우를 고려하여 테이블을 갱신한다. (A부터B의 거리 = min(A부터B의거리,A부터K를 거쳐B로 가는 거리(=A부터K까지의 거리 +K부터B가지의 거리))
성능
- 노드의 개수가 N개일 때 N개의 노드 각각에 대해 N^2의 거리를 갱신한다.
- 따라서 시간복잡도는 O(N^3)이다.
'💻 CS > 자료구조 & 알고리즘' 카테고리의 다른 글
| [자료구조] TRIE IDEA (0) | 2020.06.17 |
|---|---|
| [자료구조] Union find & an Application (0) | 2020.06.03 |
| [자료구조] Tree Traversal and Parsing (0) | 2020.06.03 |
| [자료구조] Priority Queue & Application (0) | 2020.06.02 |
| [자료구조] 2-3-4 Tree, B Tree, Red-Black Tree (0) | 2020.06.02 |